
Solve the characteristic equation, giving us the eigenvalues (2 eigenvalues for a 2x2 system) The resulting equation, using determinants, `|bb(A) - lambdabb(I)| = 0` is called the characteristic equation. `(bb(A) - )bb(v) = 0`Ĭlearly, we have a trivial solution `bb(v)=`, but in order to find any non-trivial solutions, we apply a result following from Cramer's Rule, that this equation will have a non-trivial (that is, non-zero) solution v if its coefficient determinant has value 0. This can be written using matrix notation with the identity matrix I as: We are looking for scalar values λ (numbers, not matrices) that can replace the matrix A in the expression y = Av. Our task is to find the eigenvalues λ, and eigenvectors v, such that: Set up the characteristic equation, using |A − λI| = 0 In general we can write the above matrices as: We can write those equations in matrix form as: We start with a system of two equations, as follows: There is no single eigenvector formula as such - it's more of a sset of steps that we need to go through to find the eigenvalues and eigenvectors. The resulting values form the corresponding eigenvectors of A (2 eigenvectors for a 2x2 system).Choose a convenient value for x 1, then find x 2.Substitute the eigenvalues into the two equations given by A − λ I.
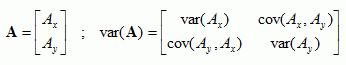
Solve the characteristic equation, giving us the eigenvalues (2 eigenvalues for a 2x2 system).
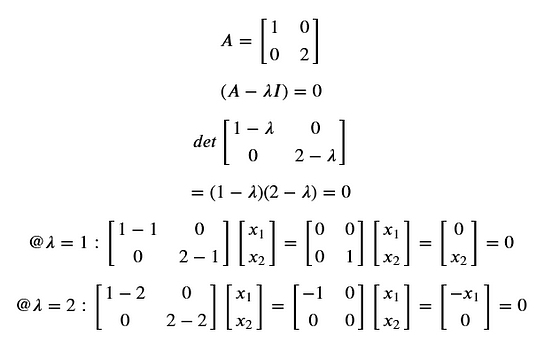
Set up the characteristic equation, using | A − λ I| = 0.
EIGEN VECTOR 2D HOW TO
First, a summary of what we're going to do: How to find the eigenvalues and eigenvectors of a 2x2 matrix The solved examples below give some insight into what these concepts mean. Eigenvalues and eigenvectors correspond to each other (are paired) for any particular matrix A. NOTE: The German word " eigen" roughly translates as "own" or "belonging to". A non-zero vector v is an eigenvector of A ifįor some number λ, called the corresponding eigenvalue. Definition of eigenvalues and eigenvectors of a matrix That example demonstrates a very important concept in engineering and science - eigenvalues and eigenvectors - which is used widely in many applications, including calculus, search engines, population studies, aeronautics and so on. On the previous page, Eigenvalues and eigenvectors - physical meaning and geometric interpretation applet we saw the example of an elastic membrane being stretched, and how this was represented by a matrix multiplication, and in special cases equivalently by a scalar multiplication. Finding eigenvalues and eigenvectors summary)


 0 kommentar(er)
0 kommentar(er)
